作者: insightcodeyk
出处: https://insightcodeyk.github.io/
声明: 本文采用以下协议进行授权: 自由转载-非商用-非衍生-保持署名|Creative Commons BY-NC-ND 3.0,转载请注明作者及出处。
1 PCA算法
PCA是一种运用K-L变换的统计分析方法,其实质是将多指标化为几个综合指标。在图像处理问题中,PCA的思想得到了很好的运用,图像多位高维数据,其样本分布规律复杂,数据难以处理,运用PCA的思想,找出几个综合变量替代原来大量且复杂的变量,可以极大的降低运算难度和处理难度。
1.1 K-L变换原理
K-L是一种最优正交变换,这一变换有去相关性的突出优点,因此可以去掉一些带有较少信息的维度,达到降维目的,其原理如下。
假设Y为N维随机变量,Y可以表示为n个基向量的加权和: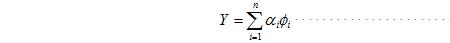
其中 为加权系数, 为基向量。
设随机向量的总体自相关矩阵为: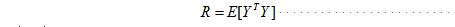
最终可得到: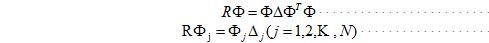
其中 是本征向量。又因为R为实对称矩阵,所以其不同本征值对应的本征向量正交。
1.2 奇异值分解定理(SVD)
在多数情况下所获得的人耳图像并不是方阵形式,行列向量并不相等,这时候就需要用到奇异值分解。对于这种mn形式的矩阵,奇异值分解法的分解形式如下: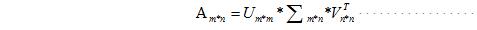
其中Amn是一个mn的矩阵,Umm是一个被称为做奇异向量的mm方阵,Σmn是一个对角线上数值为奇异值的对角矩阵,VnnT是为称为右奇异向量的nn方阵。
将人耳图像的奇异值作为特征向量是有优点的:
1.图像的奇异值较为稳定,因此当有外界干扰时,奇异值基本不变。
2.奇异值对图像的各种变化,如平移、旋转、伸缩、灰度值比率的变化有较好的鲁棒性。