作者: insightcodeyk
出处: https://insightcodeyk.github.io/
声明: 本文采用以下协议进行授权: 自由转载-非商用-非衍生-保持署名|Creative Commons BY-NC-ND 3.0,转载请注明作者及出处。
1 FDA算法简介
1.1 Fisher线性判别法(FDA)
Fisher线性判别法(FDA)是采用Fisher判别准侧函数的线性判别分析(LDA),被广泛应用于高维数据分类领域的监督型降维技术,在医学诊断,气象学,市场预测,地质勘探等领域都起到了重要的作用。其理论思想是寻找一组最佳子向量,使得样本对其投影的类内离散度最小,类间离散度最大。
1.1.1 Fisher判别
Fisher判别准则的实现思想是:寻找到一组向量,使得样本对其投影后有类内离散度小,类间离散度大的特点。在二维空间直观示意图,如下。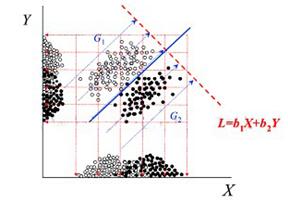
1.2 FDA用于特征提取中存在的两个问题和解决办法
问题一:小样本问题(SSS)。如上两节所述,在投影向量和投影向量矩阵的求解函数式中有一个前提条件Sw可逆,由于人耳样本图像转换成列向量后维数在大多数情况下都较高,且远远大于样本个数,这就导致了样本类内离散度矩阵Sw不可逆,这样就是无法求出最佳投影向量。针对这个问题已有一些不错的处理方法:
(1)零空间法。Chen等人提出了直接利用Sw的零空间来求解最佳投影矩阵。Sw的零空间即Sw零特征值对应的特征向量组成的子空间。他们首先利用“Pixel grouping”对原图像进行降维,计算Sw的零空间,并在零空间寻找Sb较大的特征向量作为最终投影矩阵。
(2)直接LDA(D-LDA)方法。Yu等提出的直接LDA方法,首先对Sb单位化,再对Sw对角化,从而避免了“SSS”问题。
(3)扰动法。Hong等提出的扰动法顾名思义,加上一个小的扰动k,使得新的 ,处理后 可逆,可在此基础上直接使用标准LDA方法。
(4)降维法。降维法主要有两种,其一是通过PCA进行降维,也就是本文所使用的方法,另一种是以“谱能量分析”的思想为基础增强Fisher线性判别模型法,即EFM。
问题二: DFA方法首先假设样本类服从同协方差矩阵的高斯分布,但是在人耳识别中,由于光线、角度、遮挡物等影响,图像往往不服从高斯分布。针对这一问题的处理方法有如下:
(1)非参数线性判别分析(NDA)方法。由K.Fukunage等人提出的NDA方法重新定了类间离散度矩阵SbN: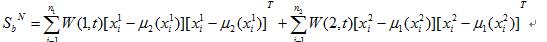
式中: 为类别j的第i个样本对应的向量,W(i,t)为权值函数, 为局部K-nn的均值向量。SbN充分利用了每个样本,并使得矩阵的秩得到提高,可以用于不符合高斯分布的问题。
(2)因为NDA算法只能应用于两类分类问题,M.Bressan等定义了一个是用于多类问题的类间离散度矩阵,使得NDA算法扩展到了多类问题。
(3)考虑到M.Bressan等人的方法丢弃了类内离散度矩阵Sw的零空间信息,Li等定义了一种也可以用于多类问题,并分别利用了Sw的主空间和零空间的类间离散度矩阵Sb的方法,非参数化子空间分析法(NSA)。
2 参考
[1]R.Duda and P.Hart. Pattern Classification and Scene Analysis[M].Wiley,New York,1973.
[2]Chen Li-Fen,Liao H-Y Mark,Ko M-T,et al.A new LDA-based face recognition system which can solve the small sample size problem[J].Pattern Recongnition,2000,33(10):1713-1726.
[3]Xiao gang Wang,Xiao ou Tang. Dual-Space Linear Discriminant Analysis for Face Recognition,IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR’04)[J],1063-6919/04,2004.